the experimental error is

LEARN STATISTICS EASILY

Learn Data Analysis Now!

What is: Experimental Error

What is experimental error.

Experimental error refers to the difference between the measured value and the true value of a quantity in scientific experiments. It is an inherent aspect of any experimental process, arising from various sources such as measurement inaccuracies, environmental factors, and limitations in the experimental design. Understanding experimental error is crucial for data analysis and interpretation in fields like statistics, data science, and research.

Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.

Types of Experimental Error

There are two primary types of experimental error: systematic error and random error. Systematic errors are consistent and repeatable inaccuracies that occur due to flaws in the measurement system or experimental setup. In contrast, random errors are unpredictable fluctuations that can arise from various sources, including human error, environmental changes, or limitations in measurement tools. Both types of errors can significantly impact the reliability of experimental results.

Systematic Error Explained

Systematic error can lead to biased results, as it consistently skews measurements in a particular direction. This type of error can often be identified and corrected through calibration of instruments or adjustments in the experimental procedure. For instance, if a scale consistently reads 0.5 grams too high, all measurements taken with that scale will be systematically biased. Recognizing and mitigating systematic errors is essential for achieving accurate and reliable data.

Random Error Explained

Random error, on the other hand, is characterized by its unpredictable nature. It can arise from various factors, such as fluctuations in environmental conditions, variations in the measurement process, or even human error during data collection. Unlike systematic errors, random errors can be reduced by increasing the number of observations or measurements, as the average of a large number of trials tends to converge on the true value. Understanding random error is vital for statistical analysis and hypothesis testing.

Impact of Experimental Error on Data Analysis

Experimental error can significantly affect the outcomes of data analysis and the conclusions drawn from experimental results. When errors are not accounted for, they can lead to incorrect interpretations and potentially flawed decisions based on the data. Researchers must employ statistical methods to quantify and minimize the impact of experimental error, ensuring that their findings are robust and reliable.

Quantifying Experimental Error

Quantifying experimental error involves calculating the uncertainty associated with measurements. This can be done using various statistical techniques, such as calculating the standard deviation, confidence intervals, and error propagation. These methods help researchers understand the degree of uncertainty in their measurements and provide a framework for making informed decisions based on the data collected.

Reducing Experimental Error

To enhance the accuracy of experimental results, researchers can implement several strategies to reduce experimental error. These include improving measurement techniques, using high-quality instruments, standardizing procedures, and conducting repeated trials. By systematically addressing potential sources of error, researchers can improve the reliability of their findings and contribute to the overall integrity of scientific research.

Role of Experimental Error in Scientific Research

Experimental error plays a critical role in scientific research, as it influences the validity and reliability of experimental findings. Acknowledging and addressing experimental error is essential for maintaining the integrity of scientific inquiry. Researchers must be transparent about the limitations of their studies and the potential sources of error, allowing for a more accurate interpretation of results and fostering trust in the scientific community.

Conclusion on Experimental Error

In summary, understanding experimental error is fundamental for anyone involved in statistics, data analysis, and data science. By recognizing the types of errors, quantifying their impact, and implementing strategies to minimize them, researchers can enhance the accuracy and reliability of their experimental results. This knowledge is crucial for making informed decisions based on data and advancing scientific knowledge.

Learn The Types

Learn About Different Types of Things and Unleash Your Curiosity

Understanding Experimental Errors: Types, Causes, and Solutions

Types of experimental errors.

In scientific experiments, errors can occur that affect the accuracy and reliability of the results. These errors are often classified into three main categories: systematic errors, random errors, and human errors. Here are some common types of experimental errors:

1. Systematic Errors

Systematic errors are consistent and predictable errors that occur throughout an experiment. They can arise from flaws in equipment, calibration issues, or flawed experimental design. Some examples of systematic errors include:

– Instrumental Errors: These errors occur due to inaccuracies or limitations of the measuring instruments used in the experiment. For example, a thermometer may consistently read temperatures slightly higher or lower than the actual value.

– Environmental Errors: Changes in environmental conditions, such as temperature or humidity, can introduce systematic errors. For instance, if an experiment requires precise temperature control, fluctuations in the room temperature can impact the results.

– Procedural Errors: Errors in following the experimental procedure can lead to systematic errors. This can include improper mixing of reagents, incorrect timing, or using the wrong formula or equation.

2. Random Errors

Random errors are unpredictable variations that occur during an experiment. They can arise from factors such as inherent limitations of measurement tools, natural fluctuations in data, or human variability. Random errors can occur independently in each measurement and can cause data points to scatter around the true value. Some examples of random errors include:

– Instrument Noise: Instruments may introduce random noise into the measurements, resulting in small variations in the recorded data.

– Biological Variability: In experiments involving living organisms, natural biological variability can contribute to random errors. For example, in studies involving human subjects, individual differences in response to a treatment can introduce variability.

– Reading Errors: When taking measurements, human observers can introduce random errors due to imprecise readings or misinterpretation of data.

3. Human Errors

Human errors are mistakes or inaccuracies that occur due to human factors, such as lack of attention, improper technique, or inadequate training. These errors can significantly impact the experimental results. Some examples of human errors include:

– Data Entry Errors: Mistakes made when recording data or entering data into a computer can introduce errors. These errors can occur due to typographical mistakes, transposition errors, or misinterpretation of results.

– Calculation Errors: Errors in mathematical calculations can occur during data analysis or when performing calculations required for the experiment. These errors can result from mathematical mistakes, incorrect formulas, or rounding errors.

– Experimental Bias: Personal biases or preconceived notions held by the experimenter can introduce bias into the experiment, leading to inaccurate results.

It is crucial for scientists to be aware of these types of errors and take measures to minimize their impact on experimental outcomes. This includes careful experimental design, proper calibration of instruments, multiple repetitions of measurements, and thorough documentation of procedures and observations.

You Might Also Like:

Patio perfection: choosing the best types of pavers for your outdoor space, a guide to types of pupusas: delicious treats from central america, exploring modern period music: from classical to jazz and beyond.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Appendix A: Treatment of Experimental Errors

• Last updated
• Save as PDF
• Page ID 435125

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Every measurement that is made in the laboratory is subject to error. An experimenter should try to minimize these errors. However, since they cannot be entirely eliminated, a means to describe and quantify the errors is needed, so that another experimenter can judge and interpret the uncertainties reported with any result. This outline defines certain terms that are important in the treatment of errors. Certain conclusions that are derived from a statistical analysis of random errors are also presented. Finally, some rules are given for discarding questionable data, for propagating errors in calculations, and for finding the best straight line through a set of graphed data.

Types of Error

There are two general classes of errors. Systematic or determinate errors are reproducible in successive measurements and may be detected and corrected. Often systematic error is due to an incorrect calibration, for example of volumetric glassware, an electronic balance or a pH meter, and causes all readings to have the same recurring error. Random or indeterminate errors are due to limitations of the measurement that are beyond the experimenter's control. They cannot be eliminated, and lead to positive and negative fluctuations in successive measurements. Examples of random errors are the fluctuations in the interpolation of the reading of a thermometer scale by different observers and the oscillations in the output of a pH meter due to electrical noise.

Accuracy and Precision

The accuracy of a result refers to how close the result is to its true value, while the precision of a result indicates its reproducibility in successive measurements. If successive measurements are in close agreement, the result has a high precision, which usually implies small random errors. If the result is in good agreement with the true value, it has high accuracy, which suggests small systematic errors.

A well-designed experiment attempts to minimize both systematic and random errors, thereby allowing both high accuracy and high precision from careful measurements. Since systematic errors are not generally manifest in successive measurements, they can be avoided only by careful calibration and consideration of all possible corrections. Random errors are indicated by the fluctuations in successive measurements. They can be quantified and treated by the methods of statistics. In the following we restrict the discussion to random errors, assuming that all systematic errors have been eliminated.

Statistical Treatment of Random Errors

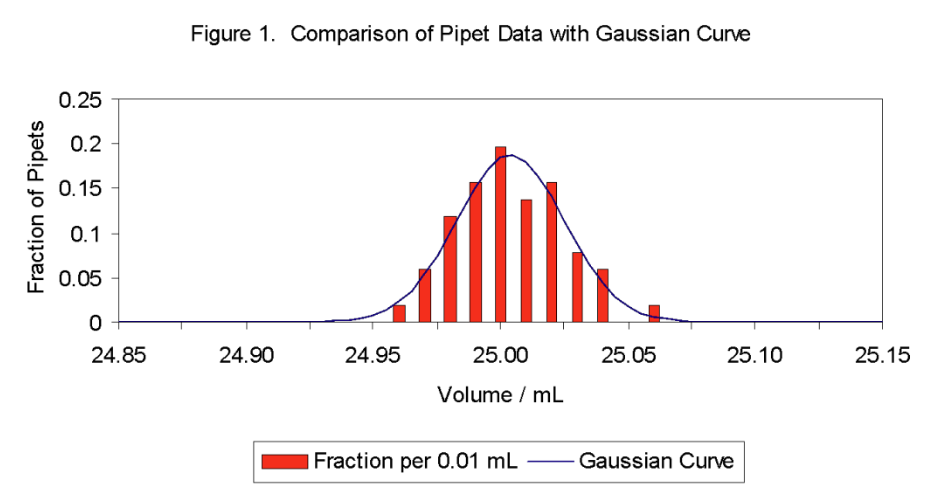
Let's consider as an example the volume of water delivered by a set of 25 mL pipets. A manufacturer produces these to deliver 25.00 mL at 20°C with a stated tolerance of ±0.03 mL. A sample of 100 pipets is tested for accuracy by measuring the delivered volumes. The column graph in Figure 1 shows the fractional number of the sampled pipets that deliver a particular volume in each 0.01 mL interval. The maximum of the column graph indicates that most of the pipets deliver between 24.995 and 25.005 mL. However, other pipets deliver lesser or greater volumes due to random variations in the manufacturing process.

The mean or average, \( \ce{x_{avg}}\), of a set of results is defined by

\( \ce{x_{avg} = \frac{\sum_{i}x_{i}}{N} } \)

where \( \ce{x_{i}}\) is an individual result and N is the total number of results. For the data in Figure 1, the mean volume is 25.0039 mL. The mean alone, however, provides no indication of the uncertainty. The same mean could have resulted from data with either more or less spread. The spread of the individual results about the mean is characterized by the sample standard deviation , s , which is given by

\( \ce{ s = ( \frac{\sum_{i} (x_{i}-x_{avg})^{2}}{N-1} )^{1/2} } \)

The pipet data has a sample standard deviation of 0.0213 mL.

The sample standard deviation gives us a quantitative measurement of the precision. To see how this works, let's imagine that we increase the number of sampled pipets. The bar graph will show less irregularities. A line connecting the tops of the bars will approach a smooth bell-shaped curve as the number of samples approaches infinity and the volume interval approaches zero. This smooth curve is called a Gaussian or normal error curve. Its formula is

\( \ce{ y(x) = \frac {1}{\sigma(2\pi)^{1/2}} exp [-\frac{(x-\mu)^{2}}{2\sigma^{2}} ] } \)

where exp[···] = e [···]  with e = 2.178..., the base of natural logarithms. For an infinite or complete data set, the mean is called \( \ce{\mu}\) (the population mean) and the standard deviation \( \ce{\sigma}\) (the population standard deviation). We can never measure \( \ce{\mu}\) and \( \ce{\sigma}\), but \( \ce{x_{avg}}\) and \( \ce{s}\) approach \( \ce{\mu}\) and \( \ce{\sigma}\), respectively, as the number of samples or measurements increases. The smooth curve in Figure 1 shows a graph of equation (3) for \( \ce{\mu}\) = 25.0039 mL and \( \ce{\sigma}\) = 0.0213 mL, as approximated by \( \ce{x_{avg}}\) and \( \ce{s}\).

The Gaussian curve gives the probability of obtaining a particular result \( \ce{x}\) for a given \( \ce{\mu}\) and \( \ce{\sigma}\). This probability is proportional to the \( \ce{y}\) value of the Gaussian curve for the particular \( \ce{x}\) value. The maximum probability occurs at the maximum of the function, which corresponds to \( \ce{x=\mu}\). Other values of \( \ce{x}\) have lower probabilities. Because of the symmetry of the curve, values of \( \ce{x}\) that deviate from \( \ce{\mu}\) by the same magnitude, i.e. , have the same \( \ce{|(x-\mu)|}\), have the same probabilities.

The significance of the standard deviation is that it measures the width of the Gaussian curve. The larger the value of \( \ce{\sigma}\), the broader the curve and the greater the probability of obtaining an \( \ce{x}\) value that deviates from \( \ce{\mu}\). One can calculate the percent of the samples or measurements that occurs in a given range from the corresponding fraction of the area under the Gaussian curve by integral calculus. Representative results are summarized in Table 1. For example, 68.3% of the samples or measurements are expected to lie between \( \ce{\mu-\sigma}\) and \( \ce{\mu+\sigma}\), and 90.0% between \( \ce{\mu-1.645\sigma}\) and \( \ce{\mu+1.645\sigma}\). Table 1. Area under Gaussian Curve

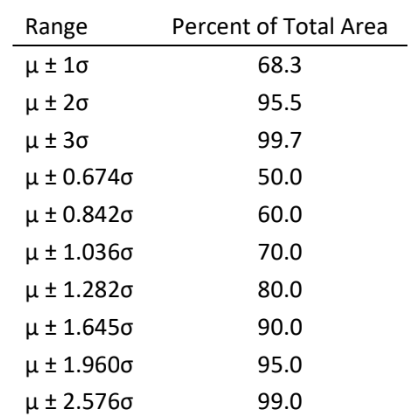
The manufacturer can thus have 90.0% confidence that some other pipet (from the identical manufacturing process) will deliver a volume in the range \( \ce{\mu \pm 1.645 \sigma} \). Estimating \( \ce {\mu = x_{avg} =} \)25.004 mL and \( \ce{\sigma = s =}\) 0.0213 mL, the manufacturer can claim that the pipets deliver 25.00 mL with a tolerance of (1.64)(0.021) = 0.03 mL. The 90% degree of confidence is hidden in this claim, and a higher degree of confidence would have correspondingly poorer (greater) tolerances. The purchaser, however, may not be told these details!

Confidence Limits

Although we cannot determine \(\ce{\mu}\) and \(\ce{\sigma}\) from a limited number of measurements, statistical analysis does allow us to obtain the confidence limits for \(\ce{\mu}\) from a limited data set. Namely, we can state to a certain probability (confidence) that \(\ce{\mu}\) will lie within certain limits of \(\ce{x_{avg}}\). These confidence limits (CL) are given by

\( \ce{CL = \pm \frac{ts}{\sqrt{N}}} \)

where \(\ce{s}\) is the sample standard deviation and N is the number of measurements. The \( \ce{\sqrt{N}} \) term in the denominator accounts for the fact that the sample mean has a greater precision than any individual measurement. 1* The factor t (called Student's t value) is given in Table 2 for several levels of confidence. The t -value for other levels of confidence can be calculated with a microcomputer spreadsheet using the built-in functions. In MS Excel, the function that returns t is TINV(\(\ce{\alpha}\), DF) where 1-\(\ce{\alpha}\) is the confidence level (for 95% confidence, \(\ce{\alpha}\) = 0.05) and DF is the degrees of freedom. The t -value can be viewed as a correction for the limited number of measurements in a data set and the associated errors in approximating \(\ce{\mu}\) and \(\ce{\sigma}\) by \(\ce{x_{avg}}\) and \(\ce{s}\), respectively. If N is infinite, the value of t for the various confidence limits in Table 2 equals the number multiplying \(\ce{\sigma}\) in the range column of Table 1 for the corresponding confidence. For example, for N infinite and 90.0% confidence, Table 2 gives t = 1.645. This agrees with the factor multiplying \(\ce{\sigma}\) for 90.0% confidence in Table 1. However, if N is finite, the value of t for a given confidence must increase as N decreases, since \(\ce{x_{avg}}\) and \(\ce{s}\) become poorer estimates of \(\ce{\mu}\) and \(\ce{\sigma}\).

* Imagine a group of data sets. For each set the sample mean is calculated. The group of means will show a scatter that is also described by a Gaussian curve. However, the width of this curve will be less than the width of the curve associated with a single data set; the standard deviation of the mean is less than the standard deviation of the data. The standard deviation in the mean, \(\ce{s_{x}}\), can be estimated from just one data set and its sample standard deviation, \(\ce{s}\), by \(\ce{s_{x}=\frac{s}{\sqrt{N}}}\). This means that the uncertainty in the mean decreases as the square-root of the number of measurements increases. Hence, to reduce the uncertainty in the mean by a factor of two, the number of measurements must be increased by a factor of four.

Estimates of \(\ce{\mu}\) and its confidence limits become important, say, in the calibration of an individual pipet. Let's assume that 10 determinations of the delivered volume for a particular pipet also yield \(\ce{x_{avg}=}\) 25.004 mL with \(\ce{s}\) = 0.0213 mL. The best estimate of the population mean (the mean from an infinite number of measurements of the delivered volume) is \(\ce{\mu = x_{avg} =}\)25.004 mL. Its 95.0% confidence limits for 10 measurements is then \(\ce{\pm \frac{ts}{\sqrt{N}} = \pm \frac{(2.262)(0.0213)}{\sqrt{10}}= \pm0.0152 } \) mL where the t value was obtained from Table 2. Accordingly, to 95.0% confidence the average volume of the particular pipet is 25.004 ± 0.015 mL. This means that there is a 95% probability that the true or population mean will lie within ±0.015 mL of 25.004 mL.

You will use the foregoing method of estimating the population or true mean and its confidence limits in many of your laboratory experiments. Typically you will make at least three measurements or determinations of a quantity. You will report the sample mean, \( \ce{x_{avg}} \), as an approximation of the true mean; the sample standard deviation, \( \ce{s}\) as an approximation of the population standard deviation; and the 95% confidence limits of the mean. The chosen confidence is that typically used when reporting scientific results. The mean is calculated from equation (1), the standard deviation from equation (2) and the confidence limits of the mean from equation (4) using the t values for 95% confidence in Table 2. Scientific calculators and microcomputer spreadsheets typically have built-in functions to calculate the sample mean and the sample standard deviation, but not confidence limits.

Sometimes a single piece of data appears inconsistent with the remaining data. For example, the questionable point may be much larger or much smaller than the remaining points. In such cases, one requires a valid method to test if the questionable point can be discarded in calculating the sample mean and standard deviation. The Q test is used to help make this decision.

Assume that the outlier (the data point in question) has a value \( \ce{x_{0}} \). Calculate the magnitude of the difference between \( \ce{x_{0}} \) and its nearest value from the remaining data (called the gap), and the magnitude of the spread of the total data including the value \( \ce{x_{0}} \) (called the range). The quantity \( \ce{Q_{Data}} \), given by

\( \ce{Q_{Data} = \frac{gap}{range}} \)

is compared with tabulated critical values of Q for a chosen confidence level. If \( \ce{Q_{Data}>Q_{Critical}} \), the outlier can be discarded to the chosen degree of confidence. The Q test is fairly stringent and not particularly helpful for small data sets if high confidence is required. It is common to use a 90% confidence for the Q test, so that any data point that has less than a 10% chance of being valid can be discarded. Values of \( \ce{Q_{Critical}} \) for 90% confidence are given in Table 3.

Let's consider an example to clarify the use of the Q test. Suppose that you make four determinations of the concentration of a solution, and that these yield 0.1155, 0.1150, 0.1148 and 0.1172 M. The mean concentration is 0.1156 M with a standard deviation of 0.0011 M. The 0.1172 M data point appears questionable since it is nearly two standard deviations away from the mean. The gap is (0.1172 - 0.1155) = 0.0017, and the range is (0.1172 - 0.1148) = 0.0024, so that \( \ce{Q_{Data}} \) = 0.0017/0.0024 = 0.71. Table 3 gives \( \ce{Q_{Critical}} \) = 0.76 for 90% confidence and four determinations. Since \( \ce{Q_{Data}<Q_{Critical}} \), the questionable point cannot be discarded. There is more than a 10% chance that the questionable point is valid.

Several caveats should be noted about the Q test. Firstly, it may be applied to only one outlier of a small data set. Secondly, even at 90% confidence some "bad" data point may be retained. If you are sure that the point is bad because of some action noted during the measurement (for example, you know that you overshot the endpoint of a titration for the particular sample during its analysis), then the point can and should be discarded. Thirdly, an apparent outlier can result in a limited data set simply from the statistical distribution of random errors, as occurred in the above example. Repeating the measurement so as to increase the data set, and thereby decrease the importance of the apparent outlier, is generally much more valuable than any statistical test.

Propagation of Errors

A quantity of interest may be a function of several independent variables, say f(x,y). It would be evaluated by performing arithmetic operations with several numbers (x and y), each of which has an associated random error. These random errors, which we denote as \(\ce{e_{x}}\) and \(\ce{e_{y}}\), may be simply estimates, standard deviations or confidence limits, so long as the same measure is used for both. How do these errors propagate in determining the corresponding error, \(\ce{e_{f}}\), in the final quantity of interest? This error is not simply the sum of the individual errors since some of these are likely to be positive and others negative, so that a certain cancellation will occur. We give below the equations determining \(\ce{e_{f}}\) for simple operations. These equations are obtained using differential calculus.

\( \ce{ f = \alpha x + \beta y } \)        with \(\ce{\alpha} \) and \( \ce{\beta} \) constants.

\( \ce {e_{f}^{2} = \alpha^{2}e_{x}^{2} + \beta^{2}e_{y}^{2} } \)

\( \ce{ f = \alpha x^{n}\beta y^{m} } \)        with \(\ce{\alpha} \), \(\ce{n} \) and \( \ce{m} \) constants.

\( \ce { \frac{e_{f}^{2}}{f^{2}} = n^{2} (\frac{e_{x}}{x})^{2} + m^{2}(\frac{e_{y}}{y})^{2} } \)

The case \( \ce{ f = \alpha x + \beta y } \) includes addition and subtraction by choosing the signs of \(\ce{\alpha} \) and \( \ce{\beta} \), while the case \( \ce{ f = \alpha x^{n}\beta y^{m} } \) includes multiplication and division by appropriate choice of the exponents. Any of the constants \(\ce{\alpha} \), \(\ce{\beta}\), \(\ce{n} \), or \( \ce{m} \) can be positive, negative or zero. The cases where \(\ce{\beta = 0}\) or \(\ce{m = 0}\), for example, correspond to the function depending on the single variable \(\ce{(x)}\). More complicated cases, involving, for example, both addition and division, can be deduced by treating the various parts or factors separately using the given equations. Two simple examples of error propagation are considered below.

Example 1.  You determine the mass (let's call this f) of a substance by first weighing a container \(\ce{(x)}\) and then the container with the substance \(\ce{(y)}\), using a balance accurate to 0.1 mg. The mass of the substance is then \(\ce{f = y ? x}\), and its error from equation (6) is

\(\ce { e_{f} = (e^{2}_{x})^{1/2} = (0.1^{2} + 0.1^{2})^{1/2} = 0.14} \) mg

since \( \ce{\alpha = \beta = 1} \) and \( \ce{ e_{x} = e_{y} = 0.1} \) mg

Example 2.  You determine the density, \(\ce{d}\), of a block of metal by separate measurements of its mass, \(\ce{m}\), and volume, \(\ce{V}\). The mass and volume are each measured four times. Their mean values with standard deviations in parentheses are \(\ce{m_{avg}}\) = 54.32 (0.05) g and \(\ce{V_{avg}}\) = 6.78 (0.02) mL. The density is 54.32/6.78 = 8.012 g/mL. The standard deviation in \(\ce{d}\), \(\ce{e_{d}}\), would be calculated from equation (7), which gives

\( \ce{ e_{d} = d[(\frac{e_{m}}{m})^{2} + (\frac{e_{V}}{V})^{2}]^{1/2} } \)

\( \ce { = 8.012 [(\frac{0.05}{54.32})^{2} + (\frac{0.02}{6.78})^{2}]^{1/2}  }\)

\( \ce{ 8.012(0.00309) = 0.025 } \) g/mL

We can also obtain the 95% confidence limits for the true density by using the 95% confidence limits for the mass and volume. For four measurements or three degrees of freedom, Table 2 gives t = 3.182. The 95% confidence limits for the mass of the block become \(\ce{ \pm \frac{(3.182)(0.05)}{\sqrt{4}} = \pm{0.08} }\) g, and for its volume \( \ce{ \pm \frac{(3.182)(0.02)}{\sqrt{4}} = 0.03}\) mL. Then,

CLd (95%)        \( \ce{ = \pm 8.012[(\frac{0.08}{54.32})^{2} + (\frac{0.03}{6.78})^{2}]^{1/2} } \)

\( \ce{ = \pm 8.012(0.0047) = \pm 0.038 } \) g/mL

Thus, there is a 95% probability that the true density of the metal block falls within \(\ce{\pm}\)0.04 g/mL of 8.01 g/mL, or there is less than a 5% probability that it is outside this range.

Example 3. Suppose that you measure some quantity x, but what you really want is \(\ce{f = x^{1/2}}\). You determine that \(\ce{x = 0.5054}\) with a standard deviation of 0.0004. Hence, \(\ce{f = (0.5054)^{1/2} = 0.7109}\). From equation (7) with \(\ce{n = 1/2}\) and \(\ce{m = 0}\), the propagated standard deviation in f becomes

\( \ce{ e_{f} = f[n^{2}(\frac{e_{x}}{x})^{2}]^{1/2} }\)

\( \ce{ 0.7109[(1/2)^{2}(\frac{0.0004}{0.5054})^{2}]^{1/2} = 0.0003 } \)

Method of Least Squares

You will often be asked to graph some experimental data, and to find the "best" straight line that represents the data. A possible approach is to visually determine the line from the graph with a straight edge, draw the line on the graph, and then measure its slope and intercept from the graph. But, will this line be the "best" line? To answer this question, we have to define what "best" means. However, even without such a definition, it is clear that the slope and intercept obtained by the visual approach are not unique, since different people would make different judgments. The least squares or linear regression method leads to unique answers for the slope and intercept of the best line.

Many scientific calculators and microcomputer spreadsheets have built-in algorithms or functions for a least squares analysis, i.e. , for obtaining the slope and intercept of the best line through a set of data points. The estimated errors (standard deviations) in the slope and intercept are also often available. You can use these functions without knowing the details of the least squares method, which require differential calculus and advanced statistics. However, you should understand its general idea. This is described in the following, sacrificing rigor for (hopefully) clarity.

Let's consider a particular experimental example. The volume of a gas is measured as a function of temperature, while maintaining the amount of gas and the pressure constant. The expected behavior of the gas follows from the ideal gas law, which is

\( \ce{PV = nRT} \)

where \(\ce{P}\) is the pressure, \(\ce{V}\) is the volume, \(\ce{n}\) is the amount in moles, \(\ce{R}\) is the ideal gas constant, and \(\ce{T}\) is the temperature in K (Kelvin). We assume that the temperature is measured in °C (Celsius), which we label t , where \(\ce{T = t + 273.15}\). The ideal gas law can be rewritten to better express the present experiment as

\(\ce{V = (\frac{nR}{P})T}\)

\( \ce{ = (\frac{nR}{P})t + (\frac{nR}{P})(273)}\)

Equation (9) has the form \( \ce {y=mx+b} \), the equation for a straight line, with \( \ce {x=t} \). Thus, a graph of V versus t for the gas should be a straight line with slope \( \ce{ m = (\frac{nR}{P}) }\) and a V-intercept at \( \ce{t=0}\) of \( \ce{ b = (\frac{nR}{P})(273) }\). The equation also shows that the volume of a gas would equal zero at \( \ce{ t = t_{0} = -273 }\), corresponding to absolute zero \( \ce{(T=0)}}\).

Even though absolute zero cannot be realized, we can calculate its temperature in °C, \(\ce{t_{0}}\), from measurements of the volume of a gas at several temperatures with constant pressure and amount of gas. What we require is the slope and intercept of the graph of  V  versus  t , since

\( \ce{ t_{0} = - \frac{(\frac{nR}{P})(273)}{(\frac{nR}{P})} = - \frac{intercept}{slope} }\)

We want the best values of the slope and intercept for this calculation. Figure 2 shows example student data for the volume of a sample of gas as a function of temperature. Both the volume (y) and temperature (x) measurements were subject to random errors, but those in the volume greatly exceeded those in the temperature. Hence, the points deviate from a straight line due mainly to the random errors in the volumes. The best line through the data points should then minimize the magnitude of the vertical (y) deviations between the experimental points and the line. Since these deviations are positive and negative, the squares of the deviations are minimized (hence, the name least squares).

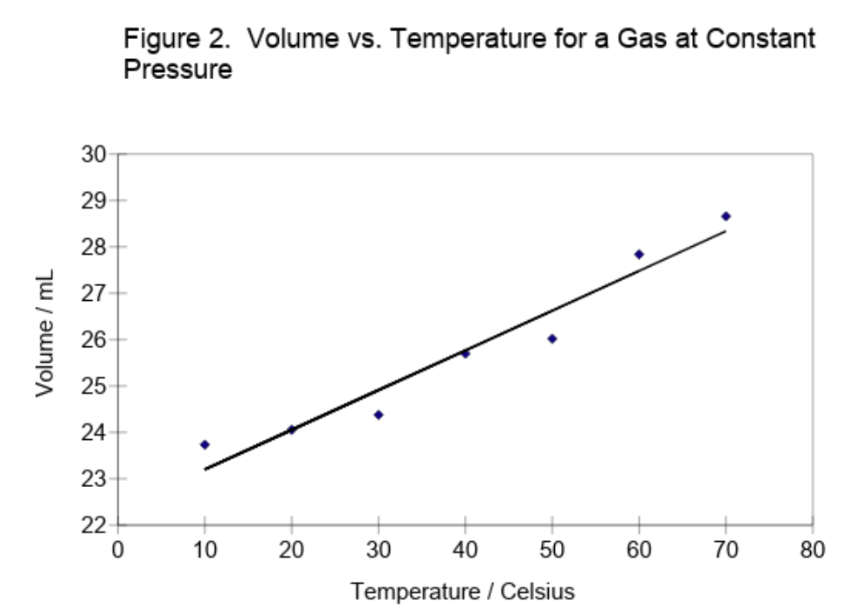
Minimizing the sum of the squares of the deviations corresponds to assuming that the observed set of volumes is the most probable set. The probability of observing a particular volume, \(\ce{V_{i}}\), for some temperature, \(\ce{t_{i}}\), is given by a Gaussian curve with the true volume \(\ce{(\mu_{v})}\) given by equation (9). The probability of obtaining the observed set of volumes is given by the product of these Gaussian curves. Maximizing this probability, so that the observed volumes are the most probable set, is equivalent to minimizing the sum of the squares of the vertical deviations. The minimization is accomplished using differential calculus, and yields equations for the slope and intercept of the best line in terms of all of the data points (all of the pairs \(\ce{V_{i}}\) and \(\ce{t_{i}}\) or, more generally, \(\ce{y_{i}}\) and \(\ce{x_{i}}\)). The resulting equations for the slope and intercept and for the standard deviations in these quantities are given in a variety of texts.* They will not be repeated here, since in this course you will use the built-in functions of a microcomputer spreadsheet to perform least squares analyses.

The line shown in Figure 2 results from a least squares fit to the experimental data. The parameters of this best-fit line and their standard deviations, obtained using a spreadsheet, are given below.

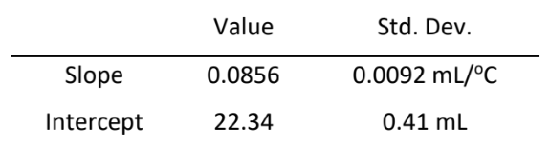
The sum of the vertical deviations, including their signs, of the experimental data points from this line equals zero, which is what one would intuitively attempt to accomplish in visually drawing the line. The sum of the deviations will always be zero for the best line, just as the sum of the deviations from an average or mean will always be zero.

The best-fit parameters yield \( \ce{ t_{0} = - (\frac{22.34}{0.0856}) = -261 }\)°C. We can obtain the uncertainty in \( \ce{t_{0}}\) by propagating the uncertainties in the slope and intercept using the formula given earlier for division involving independent variables. This is only approximately correct in the present case since the slope and intercept are correlated, and not independent. The full treatment for correlated variables, however, is beyond the scope of this introduction. The earlier formula, equation (7), gives

\( \ce{ St_{0} = 261[(\frac{0.0092}{0.0856})^{2} + (\frac{0.41}{22.34})^{2}]^{1/2} }\)

\(\ce{ 261(0.109) = 28 }\)°C

Hence, the extrapolated value of t0 agrees with the expected value within one (approximate) standard deviation.

We will now confess the truth about the "student data" in Figure 2. This was generated by adding a purely random number between -0.5 and +0.5 mL to the volume calculated for each temperature from equation (9) with \(\ce{ n = 1.0 x 10^{-3} }\) moles, \( \ce{ P = 1.0 }\) atm, and \( \ce{ R = 82.06 }\) \(\ce { \frac{mL*atm}{mol*K}} \). Hence, the expected slope is \( \ce{ (\frac{nR}{P}) = 0.08206 \frac{mL}{°C} }\), and the expected intercept is \( \ce{ (\frac{nR}{P})(273.15) = 22.414 }\) mL. The corresponding parameters derived by the least squares analysis differ from the expected values because of the random errors added to the volume. However, the derived parameters do agree with the expected or true values within one standard deviation.

Questions (Only for students who did not take 4A)

1. Multiple determinations of the percent by mass of iron in an unknown ore yield 15.31, 15.30, 15.26, 15.28 and 15.29%. Calculate:

(a) The mean percent by mass of iron;

(b) The sample standard deviation;

(c) The standard deviation of the mean;

(d) and the 95% CL of the mean.

2. For each of the following data sets, determine whether any measurement should be rejected at the 90% confidence level using the Q test.

(a) 2.8, 2.7, 2.5, 2.9, 2.6, 3.0, 2.6

(b) 97.13, 97.10, 97.20, 97.35, 97.10, 97.15

(c) 0.134, 0.120, 0.109, 0.124, 0.131, 0.119

3. A chemist determines the number of moles, n , of some gas from measurements of the pressure, P , volume, V , and temperature, T , of the gas, using the ideal gas equation of state, as \(\ce{n = \frac{PV}{RT}}\). The results of the measurements, with the estimated standard deviations in parentheses, are \(\ce{P = 0.235 (0.005)}\) atm, \(\ce{V = 1.22 (0.03)}\) L, and \(\ce{T = 310 (2)}\) K. The constant R equals \(\ce{0.08206 \frac{L*atm}{mol*K}}\). Calculate n and its estimated standard deviation.

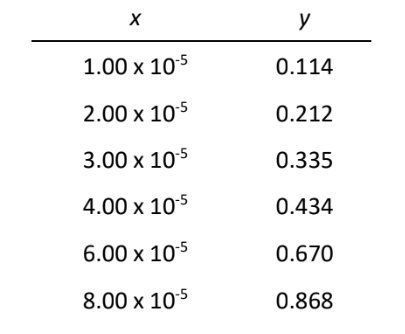
4. Use the method of least squares to find the slope, m , intercept, b , and the respective standard deviations of the best straight line, \(\ce{ y = mx + b}\), for representing the following data

• Foundations
• Write Paper

Search form

• Experiments
• Anthropology
• Self-Esteem
• Social Anxiety
• Statistics >

Experimental Error

Experimental error is unavoidable during the conduct of any experiment, mainly because of the falsifiability principle of the scientific method.

This article is a part of the guide:

• Significance 2
• Sample Size
• Experimental Probability
• Cronbach’s Alpha
• Systematic Error

Browse Full Outline

• 1 Inferential Statistics
• 2.1 Bayesian Probability
• 3.1.1 Significance 2
• 3.2 Significant Results
• 3.3 Sample Size
• 3.4 Margin of Error
• 3.5.1 Random Error
• 3.5.2 Systematic Error
• 3.5.3 Data Dredging
• 3.5.4 Ad Hoc Analysis
• 3.5.5 Regression Toward the Mean
• 4.1 P-Value
• 4.2 Effect Size
• 5.1 Philosophy of Statistics
• 6.1.1 Reliability 2
• 6.2 Cronbach’s Alpha

Therefore it is important to take steps to minimize the errors and also to understand them in order to be better able to understand the results of the experiment. This entails a study of the type and degree of errors in experimentation.

Statistical tests contain experimental errors that can be classified as either Type-I or Type-II errors. It is important to study both these effects in order to be able to manage error and report it, so that the conclusion of the experiment can be rightly interpreted.

Type I Error - False Positive Type II Error - False Negative

Type I Error

The Type I error (α-error, false positives) occurs when a the null hypothesis (H 0 ) is rejected in favor of the research hypothesis (H 1 ), when in reality the 'null' is correct. This can be understood in terms of medical tests. For example, suppose there is a test that is used to detect a disease in a person. If a Type I error occurs in the test, it means that the test will say the person is suffering from that disease even though he is healthy.

Type II Error

Type II errors (β-errors, false negatives) on the other hand, imply that we reject the research hypothesis, when in fact it is correct. In the similar example of a medical test for a disease, if a Type-II error occurs, then it means that the test will not detect the disease in the person even though he is actually suffering from it.

Hypothesis Testing

In case of Type-I errors, the research hypothesis is accepted even though the null hypothesis is correct. Type-I errors are a false positive that lead to the rejection of the null hypothesis when in fact it may be true.

When a Type-II error occurs, the research hypothesis is not detected as the correct conclusion and is therefore passed off. In terms of the null hypothesis, this kind of an error might lead to accepting the null hypothesis when in fact it is false.

The significance level refers only to the Type-I error. This is because we ask the question "What is the probability that the correlation we observed is purely by chance?" and when this question yields an answer of below a significance level (typically 5% or 1%), we state that the result wasn't a chance process and that the parameters under study are indeed related.

Reason for Errors

Scientific experiments involve a different type of error analysis than a statistical experiment. In science, experimental errors may be caused due to human inaccuracies like a wrong experimental setup in a science experiment or choosing the wrong set of people for a social experiment .

Systematic error refers to that error which is inherent in the system of experimentation. For example, if you want to calculate the value of acceleration due to gravity by swinging a pendulum , then your result will invariably be affected by air resistance, friction at the point of suspension and finite mass of the thread.

Random errors occur because it is impossible to practically achieve infinite precision. Since the value is higher or lower in a random fashion, averaging several readings will reduce random errors.

• Psychology 101
• Flags and Countries
• Capitals and Countries

Siddharth Kalla (Apr 25, 2009). Experimental Error. Retrieved Jan 10, 2025 from Explorable.com: https://explorable.com/experimental-error

You Are Allowed To Copy The Text

The text in this article is licensed under the Creative Commons-License Attribution 4.0 International (CC BY 4.0) .

This means you're free to copy, share and adapt any parts (or all) of the text in the article, as long as you give appropriate credit and provide a link/reference to this page.

That is it. You don't need our permission to copy the article; just include a link/reference back to this page. You can use it freely (with some kind of link), and we're also okay with people reprinting in publications like books, blogs, newsletters, course-material, papers, wikipedia and presentations (with clear attribution).

Want to stay up to date? Follow us!

Save this course for later.

Don't have time for it all now? No problem, save it as a course and come back to it later.

Footer bottom

• Privacy Policy

• Subscribe to our RSS Feed
• Like us on Facebook
• Follow us on Twitter