Experimental vs Quasi-Experimental Design: Which to Choose?
Here’s a table that summarizes the similarities and differences between an experimental and a quasi-experimental study design:

What is a quasi-experimental design?
A quasi-experimental design is a non-randomized study design used to evaluate the effect of an intervention. The intervention can be a training program, a policy change or a medical treatment.
Unlike a true experiment, in a quasi-experimental study the choice of who gets the intervention and who doesn’t is not randomized. Instead, the intervention can be assigned to participants according to their choosing or that of the researcher, or by using any method other than randomness.
Having a control group is not required, but if present, it provides a higher level of evidence for the relationship between the intervention and the outcome.
(for more information, I recommend my other article: Understand Quasi-Experimental Design Through an Example ) .
Examples of quasi-experimental designs include:
- One-Group Posttest Only Design
- Static-Group Comparison Design
- One-Group Pretest-Posttest Design
- Separate-Sample Pretest-Posttest Design
What is an experimental design?
An experimental design is a randomized study design used to evaluate the effect of an intervention. In its simplest form, the participants will be randomly divided into 2 groups:
- A treatment group: where participants receive the new intervention which effect we want to study.
- A control or comparison group: where participants do not receive any intervention at all (or receive some standard intervention).
Randomization ensures that each participant has the same chance of receiving the intervention. Its objective is to equalize the 2 groups, and therefore, any observed difference in the study outcome afterwards will only be attributed to the intervention – i.e. it removes confounding.
(for more information, I recommend my other article: Purpose and Limitations of Random Assignment ).
Examples of experimental designs include:
- Posttest-Only Control Group Design
- Pretest-Posttest Control Group Design
- Solomon Four-Group Design
- Matched Pairs Design
- Randomized Block Design
When to choose an experimental design over a quasi-experimental design?
Although many statistical techniques can be used to deal with confounding in a quasi-experimental study, in practice, randomization is still the best tool we have to study causal relationships.
Another problem with quasi-experiments is the natural progression of the disease or the condition under study — When studying the effect of an intervention over time, one should consider natural changes because these can be mistaken with changes in outcome that are caused by the intervention. Having a well-chosen control group helps dealing with this issue.
So, if losing the element of randomness seems like an unwise step down in the hierarchy of evidence, why would we ever want to do it?
This is what we’re going to discuss next.
When to choose a quasi-experimental design over a true experiment?
The issue with randomness is that it cannot be always achievable.
So here are some cases where using a quasi-experimental design makes more sense than using an experimental one:
- If being in one group is believed to be harmful for the participants , either because the intervention is harmful (ex. randomizing people to smoking), or the intervention has a questionable efficacy, or on the contrary it is believed to be so beneficial that it would be malevolent to put people in the control group (ex. randomizing people to receiving an operation).
- In cases where interventions act on a group of people in a given location , it becomes difficult to adequately randomize subjects (ex. an intervention that reduces pollution in a given area).
- When working with small sample sizes , as randomized controlled trials require a large sample size to account for heterogeneity among subjects (i.e. to evenly distribute confounding variables between the intervention and control groups).
Further reading
- Statistical Software Popularity in 40,582 Research Papers
- Checking the Popularity of 125 Statistical Tests and Models
- Objectives of Epidemiology (With Examples)
- 12 Famous Epidemiologists and Why
True experiment vs Quasi-experiment: What’s the difference?

There are several different approaches to experiment methodologies. Each is designed to meet the different requirements, scopes, and limitations of the experiment project at hand. Two of the most common experiment types are ‘true’ and ‘quasi.’ But what exactly are these, what purpose do they meet, and what are their differences?
This guide will explore true experiments vs. quasi-experiments and what you need to know if you’re learning about them for the first time.
Why are there different experiment methodologies?
Before we go any further, why are there different experiment types? Because experiment conditions can vary significantly, and some will present challenges. These challenges can affect how you collect data, as well as the data’s robustness, reliability, and quality .
This all comes back to why we run experiments. They examine cause-and-effect relationships and the phenomena that result—and show if these relationships are true or false.
You manipulate one or more variables that might affect the result of your experiment. These are called independent variables. You then have dependent variables, which you measure to check if your manipulation of an independent variable has had an effect.
These changing variables are key to running experiments effectively and getting reliable, robust data. But you can't manage and control all independent variables.
But before we discuss how experiment design addresses these challenges, let’s explore the baseline type of experiment.
What is a true experiment?
A true experiment is generally the preferred type of experiment design—you could see it as an experiment standard. This is because you can control all the variables affecting your results.
You use a control and experiment group to create data that only differs by a specific manipulation. The control group isn't affected by any independent variables, while the experimental group(s) (or treatment group) is.
This means you can compare the results of your control and experimental groups. Then, you can see the impact of independent variables that define the groups.
In a true experiment, the participants are randomly assigned to either the control or experimental group. This is to produce accurate results that show any cause-and-effect relationships being studied. It also helps to mitigate any bias or other variables that could skew results.
What is a quasi-experiment?
A quasi-experiment is similar to a true experiment. It aims to establish cause-and-effect relationships between a controlled independent variable and a dependent variable. But in quasi-experiments, you don’t randomly assign control and experimental groups.
Instead, you assign participants to groups based on predetermined, non-random criteria. This means that control groups aren't always necessary for quasi-experiments. But they're often included in different, non-randomized ways.
A quasi-experiment is an alternative to true experiments when there are practical or ethical reasons, as well as conflicts of interest, why participants can’t be randomly assigned to experiment groups.
The key difference between true and quasi-experiments
The key difference between true and quasi-experiments is how you assign participants to treatment groups. For true experiments, you do this randomly. For quasi-experiments, you do this with specific controls in mind.
As a result, quasi-experiment researchers can have more control over the treatment, which is the variable you're manipulating. Again, you might do this for ethical and practical reasons.
Examples of true vs quasi-experiments
Let’s see true and quasi-experiments in action.
True experiment example
You select participants with hay fever for your experiment. Then you randomly assigned them to the treatment and control groups. The control group gets a placebo, whereas the treatment group gets allergy medication. You collect data from both groups and analyze it to see how effective the allergy medication was.
Quasi-experiment example
You want to investigate the effects of a new reading program on literacy development among elementary school students. Instead of randomly assigning students to the program, you compare two existing groups:
- Students from a school that has already implemented the program (treatment group).
- Students from a similar school that uses a traditional reading curriculum (control group).
The groups are naturally formed based on their schools, not randomly assigned. You collect data from both groups and analyze it to assess the impact of the new reading program.
Effective experimental design requires careful consideration when employing the experiment type. Two of these experiment types, true and quasi, both have the same end goal but achieve this in different ways. This is because the random-assignment methodology typical to true experiments isn't suitable for all use cases.
Easily find the participants you need for your next experiment with Prolific. Choose from our pool of 200k+ active, vetted, and engaged participants and collect quality data in hours, not weeks. Get started for free .
You might also like

Building a better world with better data.

Follow us on
All Rights Reserved Prolific 2024

Login | Register
- Editorial Team
- Start Submission
- Become a Reviewer
- Harvard Citation Style
- Vancouver Citation Style
- APA Citation Style
- Download RIS
- Download BibTeX

True and Quasi-Experimental Designs
- Barry Gribbons
- Joan Herman
Accessed 296,768 times on https://pareonline.net from November 13, 1999 to December 31, 2019. For downloads from January 1, 2020 forward, please click on the PlumX Metrics link to the right.
Keywords: *Comparative Analysis; *Control Groups; Evaluation Methods; Evaluation Utilization; *Experiments; Measurement Techniques; *Pretests Posttests; *Quasiexperimental Design; Sampling; Selection, *Comparative Analysis, *Control Groups, Evaluation Methods, Evaluation Utilization, *Experiments, Measurement Techniques, *Pretests Posttests, *Quasiexperimental Design, Sampling, Selection
Gribbons, B. & Herman, J., (1996) “True and Quasi-Experimental Designs”, Practical Assessment, Research, and Evaluation 5(1): 14. doi: https://doi.org/10.7275/fs4z-nb61
Downloads: Download PDF View PDF
537 Downloads
Published on 02 jan 1996, creative commons attribution-noncommercial-noderivatives 4.0, harvard-style citation.
Gribbons, B & Herman, J. (1996) 'True and Quasi-Experimental Designs', Practical Assessment, Research, and Evaluation . 5(1) doi: 10.7275/fs4z-nb61
Show: Vancouver Citation Style | APA Citation Style
Vancouver-Style Citation
Gribbons, B & Herman, J. True and Quasi-Experimental Designs. Practical Assessment, Research, and Evaluation. 1996 1; 5(1) doi: 10.7275/fs4z-nb61
Show: Harvard Citation Style | APA Citation Style
APA-Style Citation
Gribbons, B & Herman, J. (1996, 1 2). True and Quasi-Experimental Designs. Practical Assessment, Research, and Evaluation 5(1) doi: 10.7275/fs4z-nb61
Show: Harvard Citation Style | {% trans 'Vancouver Citation Style' %}
Non Specialist Summary
This article has no summary

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
7.3 Quasi-Experimental Research
Learning objectives.
- Explain what quasi-experimental research is and distinguish it clearly from both experimental and correlational research.
- Describe three different types of quasi-experimental research designs (nonequivalent groups, pretest-posttest, and interrupted time series) and identify examples of each one.
The prefix quasi means “resembling.” Thus quasi-experimental research is research that resembles experimental research but is not true experimental research. Although the independent variable is manipulated, participants are not randomly assigned to conditions or orders of conditions (Cook & Campbell, 1979). Because the independent variable is manipulated before the dependent variable is measured, quasi-experimental research eliminates the directionality problem. But because participants are not randomly assigned—making it likely that there are other differences between conditions—quasi-experimental research does not eliminate the problem of confounding variables. In terms of internal validity, therefore, quasi-experiments are generally somewhere between correlational studies and true experiments.
Quasi-experiments are most likely to be conducted in field settings in which random assignment is difficult or impossible. They are often conducted to evaluate the effectiveness of a treatment—perhaps a type of psychotherapy or an educational intervention. There are many different kinds of quasi-experiments, but we will discuss just a few of the most common ones here.
Nonequivalent Groups Design
Recall that when participants in a between-subjects experiment are randomly assigned to conditions, the resulting groups are likely to be quite similar. In fact, researchers consider them to be equivalent. When participants are not randomly assigned to conditions, however, the resulting groups are likely to be dissimilar in some ways. For this reason, researchers consider them to be nonequivalent. A nonequivalent groups design , then, is a between-subjects design in which participants have not been randomly assigned to conditions.
Imagine, for example, a researcher who wants to evaluate a new method of teaching fractions to third graders. One way would be to conduct a study with a treatment group consisting of one class of third-grade students and a control group consisting of another class of third-grade students. This would be a nonequivalent groups design because the students are not randomly assigned to classes by the researcher, which means there could be important differences between them. For example, the parents of higher achieving or more motivated students might have been more likely to request that their children be assigned to Ms. Williams’s class. Or the principal might have assigned the “troublemakers” to Mr. Jones’s class because he is a stronger disciplinarian. Of course, the teachers’ styles, and even the classroom environments, might be very different and might cause different levels of achievement or motivation among the students. If at the end of the study there was a difference in the two classes’ knowledge of fractions, it might have been caused by the difference between the teaching methods—but it might have been caused by any of these confounding variables.
Of course, researchers using a nonequivalent groups design can take steps to ensure that their groups are as similar as possible. In the present example, the researcher could try to select two classes at the same school, where the students in the two classes have similar scores on a standardized math test and the teachers are the same sex, are close in age, and have similar teaching styles. Taking such steps would increase the internal validity of the study because it would eliminate some of the most important confounding variables. But without true random assignment of the students to conditions, there remains the possibility of other important confounding variables that the researcher was not able to control.
Pretest-Posttest Design
In a pretest-posttest design , the dependent variable is measured once before the treatment is implemented and once after it is implemented. Imagine, for example, a researcher who is interested in the effectiveness of an antidrug education program on elementary school students’ attitudes toward illegal drugs. The researcher could measure the attitudes of students at a particular elementary school during one week, implement the antidrug program during the next week, and finally, measure their attitudes again the following week. The pretest-posttest design is much like a within-subjects experiment in which each participant is tested first under the control condition and then under the treatment condition. It is unlike a within-subjects experiment, however, in that the order of conditions is not counterbalanced because it typically is not possible for a participant to be tested in the treatment condition first and then in an “untreated” control condition.
If the average posttest score is better than the average pretest score, then it makes sense to conclude that the treatment might be responsible for the improvement. Unfortunately, one often cannot conclude this with a high degree of certainty because there may be other explanations for why the posttest scores are better. One category of alternative explanations goes under the name of history . Other things might have happened between the pretest and the posttest. Perhaps an antidrug program aired on television and many of the students watched it, or perhaps a celebrity died of a drug overdose and many of the students heard about it. Another category of alternative explanations goes under the name of maturation . Participants might have changed between the pretest and the posttest in ways that they were going to anyway because they are growing and learning. If it were a yearlong program, participants might become less impulsive or better reasoners and this might be responsible for the change.
Another alternative explanation for a change in the dependent variable in a pretest-posttest design is regression to the mean . This refers to the statistical fact that an individual who scores extremely on a variable on one occasion will tend to score less extremely on the next occasion. For example, a bowler with a long-term average of 150 who suddenly bowls a 220 will almost certainly score lower in the next game. Her score will “regress” toward her mean score of 150. Regression to the mean can be a problem when participants are selected for further study because of their extreme scores. Imagine, for example, that only students who scored especially low on a test of fractions are given a special training program and then retested. Regression to the mean all but guarantees that their scores will be higher even if the training program has no effect. A closely related concept—and an extremely important one in psychological research—is spontaneous remission . This is the tendency for many medical and psychological problems to improve over time without any form of treatment. The common cold is a good example. If one were to measure symptom severity in 100 common cold sufferers today, give them a bowl of chicken soup every day, and then measure their symptom severity again in a week, they would probably be much improved. This does not mean that the chicken soup was responsible for the improvement, however, because they would have been much improved without any treatment at all. The same is true of many psychological problems. A group of severely depressed people today is likely to be less depressed on average in 6 months. In reviewing the results of several studies of treatments for depression, researchers Michael Posternak and Ivan Miller found that participants in waitlist control conditions improved an average of 10 to 15% before they received any treatment at all (Posternak & Miller, 2001). Thus one must generally be very cautious about inferring causality from pretest-posttest designs.
Does Psychotherapy Work?
Early studies on the effectiveness of psychotherapy tended to use pretest-posttest designs. In a classic 1952 article, researcher Hans Eysenck summarized the results of 24 such studies showing that about two thirds of patients improved between the pretest and the posttest (Eysenck, 1952). But Eysenck also compared these results with archival data from state hospital and insurance company records showing that similar patients recovered at about the same rate without receiving psychotherapy. This suggested to Eysenck that the improvement that patients showed in the pretest-posttest studies might be no more than spontaneous remission. Note that Eysenck did not conclude that psychotherapy was ineffective. He merely concluded that there was no evidence that it was, and he wrote of “the necessity of properly planned and executed experimental studies into this important field” (p. 323). You can read the entire article here:
http://psychclassics.yorku.ca/Eysenck/psychotherapy.htm
Fortunately, many other researchers took up Eysenck’s challenge, and by 1980 hundreds of experiments had been conducted in which participants were randomly assigned to treatment and control conditions, and the results were summarized in a classic book by Mary Lee Smith, Gene Glass, and Thomas Miller (Smith, Glass, & Miller, 1980). They found that overall psychotherapy was quite effective, with about 80% of treatment participants improving more than the average control participant. Subsequent research has focused more on the conditions under which different types of psychotherapy are more or less effective.

In a classic 1952 article, researcher Hans Eysenck pointed out the shortcomings of the simple pretest-posttest design for evaluating the effectiveness of psychotherapy.
Wikimedia Commons – CC BY-SA 3.0.
Interrupted Time Series Design
A variant of the pretest-posttest design is the interrupted time-series design . A time series is a set of measurements taken at intervals over a period of time. For example, a manufacturing company might measure its workers’ productivity each week for a year. In an interrupted time series-design, a time series like this is “interrupted” by a treatment. In one classic example, the treatment was the reduction of the work shifts in a factory from 10 hours to 8 hours (Cook & Campbell, 1979). Because productivity increased rather quickly after the shortening of the work shifts, and because it remained elevated for many months afterward, the researcher concluded that the shortening of the shifts caused the increase in productivity. Notice that the interrupted time-series design is like a pretest-posttest design in that it includes measurements of the dependent variable both before and after the treatment. It is unlike the pretest-posttest design, however, in that it includes multiple pretest and posttest measurements.
Figure 7.5 “A Hypothetical Interrupted Time-Series Design” shows data from a hypothetical interrupted time-series study. The dependent variable is the number of student absences per week in a research methods course. The treatment is that the instructor begins publicly taking attendance each day so that students know that the instructor is aware of who is present and who is absent. The top panel of Figure 7.5 “A Hypothetical Interrupted Time-Series Design” shows how the data might look if this treatment worked. There is a consistently high number of absences before the treatment, and there is an immediate and sustained drop in absences after the treatment. The bottom panel of Figure 7.5 “A Hypothetical Interrupted Time-Series Design” shows how the data might look if this treatment did not work. On average, the number of absences after the treatment is about the same as the number before. This figure also illustrates an advantage of the interrupted time-series design over a simpler pretest-posttest design. If there had been only one measurement of absences before the treatment at Week 7 and one afterward at Week 8, then it would have looked as though the treatment were responsible for the reduction. The multiple measurements both before and after the treatment suggest that the reduction between Weeks 7 and 8 is nothing more than normal week-to-week variation.
Figure 7.5 A Hypothetical Interrupted Time-Series Design
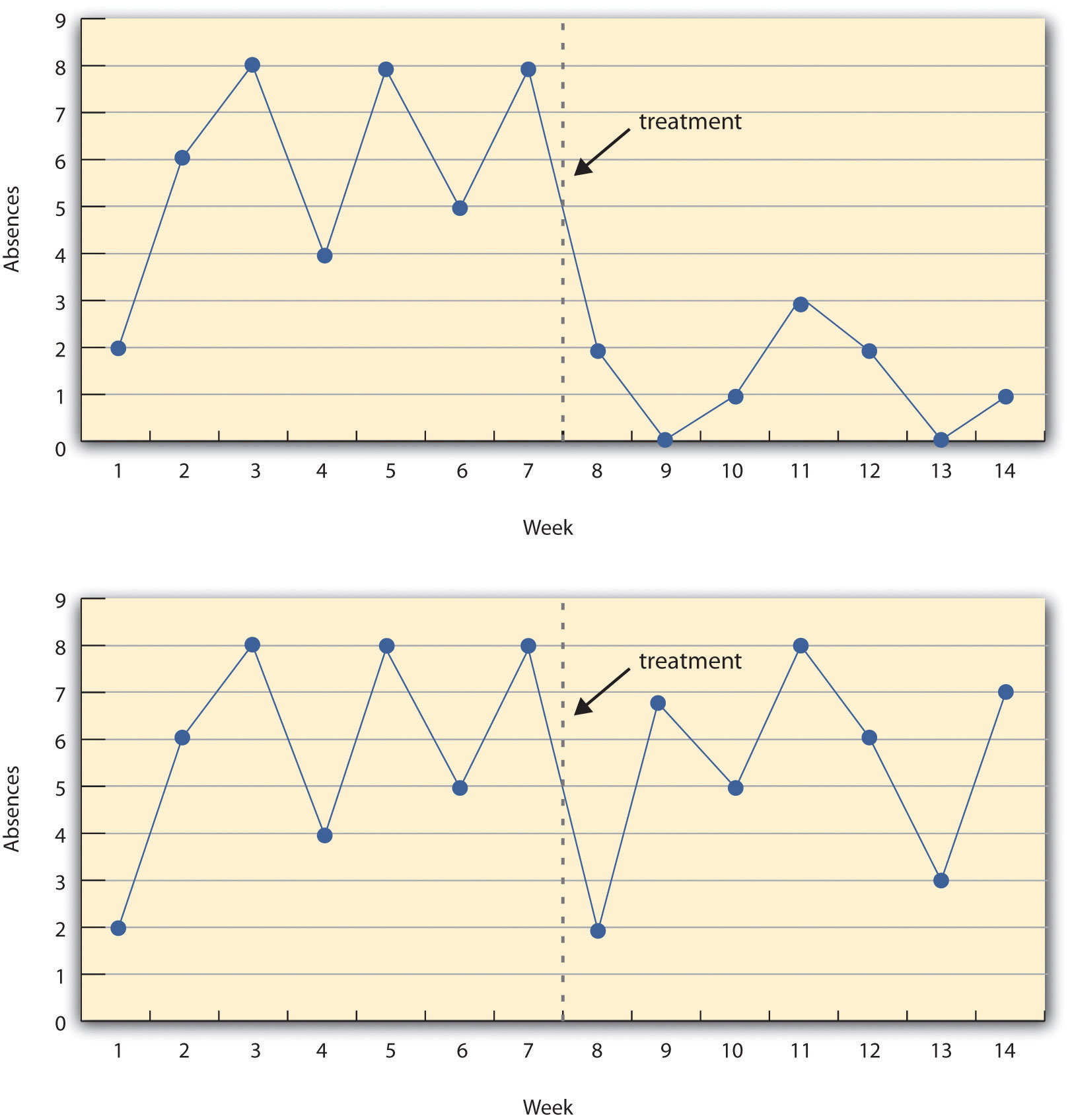
The top panel shows data that suggest that the treatment caused a reduction in absences. The bottom panel shows data that suggest that it did not.
Combination Designs
A type of quasi-experimental design that is generally better than either the nonequivalent groups design or the pretest-posttest design is one that combines elements of both. There is a treatment group that is given a pretest, receives a treatment, and then is given a posttest. But at the same time there is a control group that is given a pretest, does not receive the treatment, and then is given a posttest. The question, then, is not simply whether participants who receive the treatment improve but whether they improve more than participants who do not receive the treatment.
Imagine, for example, that students in one school are given a pretest on their attitudes toward drugs, then are exposed to an antidrug program, and finally are given a posttest. Students in a similar school are given the pretest, not exposed to an antidrug program, and finally are given a posttest. Again, if students in the treatment condition become more negative toward drugs, this could be an effect of the treatment, but it could also be a matter of history or maturation. If it really is an effect of the treatment, then students in the treatment condition should become more negative than students in the control condition. But if it is a matter of history (e.g., news of a celebrity drug overdose) or maturation (e.g., improved reasoning), then students in the two conditions would be likely to show similar amounts of change. This type of design does not completely eliminate the possibility of confounding variables, however. Something could occur at one of the schools but not the other (e.g., a student drug overdose), so students at the first school would be affected by it while students at the other school would not.
Finally, if participants in this kind of design are randomly assigned to conditions, it becomes a true experiment rather than a quasi experiment. In fact, it is the kind of experiment that Eysenck called for—and that has now been conducted many times—to demonstrate the effectiveness of psychotherapy.
Key Takeaways
- Quasi-experimental research involves the manipulation of an independent variable without the random assignment of participants to conditions or orders of conditions. Among the important types are nonequivalent groups designs, pretest-posttest, and interrupted time-series designs.
- Quasi-experimental research eliminates the directionality problem because it involves the manipulation of the independent variable. It does not eliminate the problem of confounding variables, however, because it does not involve random assignment to conditions. For these reasons, quasi-experimental research is generally higher in internal validity than correlational studies but lower than true experiments.
- Practice: Imagine that two college professors decide to test the effect of giving daily quizzes on student performance in a statistics course. They decide that Professor A will give quizzes but Professor B will not. They will then compare the performance of students in their two sections on a common final exam. List five other variables that might differ between the two sections that could affect the results.
Discussion: Imagine that a group of obese children is recruited for a study in which their weight is measured, then they participate for 3 months in a program that encourages them to be more active, and finally their weight is measured again. Explain how each of the following might affect the results:
- regression to the mean
- spontaneous remission
Cook, T. D., & Campbell, D. T. (1979). Quasi-experimentation: Design & analysis issues in field settings . Boston, MA: Houghton Mifflin.
Eysenck, H. J. (1952). The effects of psychotherapy: An evaluation. Journal of Consulting Psychology, 16 , 319–324.
Posternak, M. A., & Miller, I. (2001). Untreated short-term course of major depression: A meta-analysis of studies using outcomes from studies using wait-list control groups. Journal of Affective Disorders, 66 , 139–146.
Smith, M. L., Glass, G. V., & Miller, T. I. (1980). The benefits of psychotherapy . Baltimore, MD: Johns Hopkins University Press.
Research Methods in Psychology Copyright © 2016 by University of Minnesota is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

IMAGES