a case study on mathematics

Search form

• Travel & Maps
• Our Building
• Supporting Mathematics
• Art and Oxford Mathematics
• Equality, Diversity & Inclusion
• Undergraduate Study
• Postgraduate Study
• Current Students
• Research Groups

Case Studies

• Faculty Books
• Oxford Mathematics Alphabet
• Oxford Online Maths Club
• Oxford Maths Festival
• Privacy Statement
• It All Adds Up
• Problem Solving Matters
• PROMYS Europe
• Oxfordshire Maths Masterclasses
• Outreach Information
• Mailing List
• Key Contacts
• People List
• A Global Department
• Research Fellowship Programmes
• Professional Services Teams
• Conference Facilities
• Public Lectures & Events
• Departmental Seminars & Events
• Special Lectures
• Conferences
• Summer Schools
• Past Events
• Alumni Newsletters
• Info for Event Organisers & Attendees

The explosive secret of the squirting cucumber

New technique enhances predictions of ocean health and carbon cycles

Gravitational Spin Degrees of Freedom - a case study by Seyed Faroogh Moosavian

Coming out of their shell: how the natural world is teaching mathematicians about geometry

Additive versus multiplicative structure over integers - a case study by Akshat Mudgal

Software solutions to bridge the ‘outcome–impact gap': helping industry use mathematical models

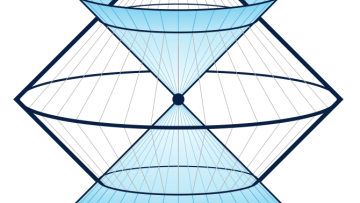
Carrollian holograms - a case study by Romain Ruzziconi

One of the most important questions in theoretical physics is finding a theory of quantum gravity, which could help us address fundamental questions about our world, related to what is inside a black hole, or what is the origin of the universe. Several approaches have been developed over the past decades to tackle this problem, with string theory being a leading candidate due to its potential to unify the laws of physics.

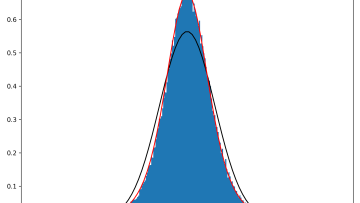
On a random model for the Möbius function and its properties - a case study by Ofir Gorodetsky

In this case study I report on a collaboration with Mo Dick Wong (Durham University), in the area of analytic and probabilistic number theory. We studied questions on a random model for the Möbius $\mu$ function. This function is one of the most elusive functions in number theory, and encodes deep questions on primes. Let's define it properly.

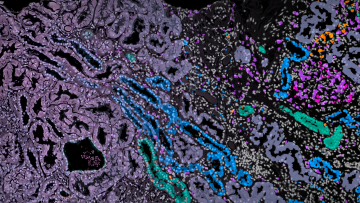
Topology and medicine combine to tackle kidney disease

Globally kidney disease is forecast to be the 5 th leading cause of death by 2040, and in the UK more than 3 million people are living with the most severe stages of chronic kidney disease. Chronic kidney disease is often due to autoimmune damage to the filtration units of the kidney, known as the glomeruli, which can occur in lupus, a disease which disproportionally affects women and people of non-white ethnicities, groups often underrepresented in research.

Learning to Adapt - Personalising Cancer Treatment Schedules using Deep Reinforcement Learning

One of the greatest challenges in cancer treatment is maximising the response to a given drug - how can doctors get the greatest impact for the patient from the drug? 

Traditionally, the answer to this has been ‘maximum tolerated dose’ (MTD) therapy, where the patient continually receives a high drug dose, with no breaks in treatment. 

Algebraic Identifiability of Partial Differential Equation Models - a case study by Hamid Rahkooy

Systems of differential equations have a key role in biological and chemical models. These models come with parameters that show the model’s dependency on the environmental effects and often have unknown values. Model simulations from observation are desired not to be affected by the values of the parameters. In other words, we would like the parameters to be identifiable from the input-output behaviour of the system.

Measuring noncommutative algebras - a new Bernstein's inequality

In mathematics, as in footwear, order matters. Putting on your socks before your shoes produces a different result to putting on your shoes before your socks. This means that the two operations 'putting on socks' and 'putting on shoes' are noncommutative . Noncommutative structures are widespread in mathematics, appearing in subjects ranging from group theory to analysis and differential equations.

Mathematics everywhere

We all know that mathematical activity goes on nowadays in a great variety of settings – not just in academia, but across the whole range of industry, education, and beyond.   This diversity in mathematics is by no means new, and yet the study of the history of mathematics has often failed to capture it.   

Holographic duals of Argyres–Douglas theories - a case study by Christopher Couzens

Holography is one of a set of powerful tools which theoretical physicists use to understand the fundamental aspects of nature. The holographic principle states that the entire information content of a theory of quantum gravity in some volume is equivalent (or dual) to a theory living at the boundary of the volume without gravity. The boundary degrees of freedom encode all the bulk degrees of freedom and their dynamics and vice versa.

Inheritance of nontrivial dynamics in chemical reaction networks - a case study by Murad Banaji

Systems of chemical reactions figure prominently in models throughout the natural sciences. Biology in particular gives rise to hugely complicated reaction networks which, somehow, perform intricate and delicate functions. How do we make sense of these complex networks, and try to understand the relationships between their structure and function? 

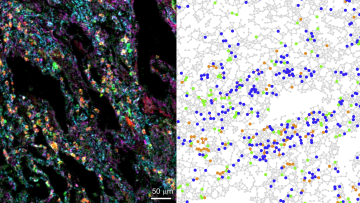
Understanding lung damage in COVID-19 patients

Mathematical modelling played a key role in describing the spread of the COVID-19 pandemic; now a different kind of maths is helping us understand how immune cells interact in the lungs of patients with severe COVID-19.

In a damaged lung with a massive immune cell infiltrate, as seen with severe COVID-19 infection, it can be difficult to figure out which cells are involved in causing lung injury. 

From natural philosophy to applied mathematics - 400 years of Sedleian Professors

For the first several centuries of its existence, an education at the University of Oxford entailed a basic grounding in a range of different subjects, rather than the specialised study of a single discipline.  The goal was to turn out well-rounded individuals rather than narrow experts.  Nevertheless, the university often tried, wherever possible, to provide advanced instruction in specific areas for those students who were interested. 

Beyond the Riemann hypothesis — primes and smooth numbers

In this case study we'll highlight new world records, going 23% beyond the Riemann Hypothesis. To explain, we start with the (last digit of) prime numbers : \[ {\color{blue}{\bf 2}}, {\color{green}{\bf3}}, {\color{orange}{\bf5}}, {\color{red}{\bf7}}, 1{\bf1}, 1{\color{green}{\bf3}}, 1{\color{red}{\bf7}}, 1{\color{purple}{\bf9}}, 2{\color{green}{\bf3}},\ldots \] After some thought, we may realize that no such last digit may be even (after ${\color{blue}{\bf 2}}$ itself), else the whole number is even; nor may ${\color{orange}{\bf5}}$ appear again.

• EXPLORE Random Article
• Happiness Hub

How to Write a Case Study on Mathematics

Last Updated: September 15, 2021

wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, volunteer authors worked to edit and improve it over time. This article has been viewed 27,476 times.

The aim of a well-written case study in Mathematics is to provide guides and teachers with important information on any number of situations that are problematic. These could be classroom specific or something huger. As a student, your case study should articulate your research goals very carefully and then go on to give good methods and a proper conclusion. Writing a math case study could be difficult but it will help you earn good grades and ensure that your guides and teachers know that you're taking your courses seriously.

Here's how you can write a good case study and ensure that you get the marks you deserve:

Community Q&A

You Might Also Like

• http://www.bestcustomwriting.com/blog/case-study-writing
• http://www.uaf.edu/mcc/award-recognition-and-oth/Math-in-a-Cultural-Context-Two-Case-Studies-of-a-Successful-Culturally-Based-Math-Project.pdf

About this article

Did this article help you.

• About wikiHow
• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Home » Case Studies » Mathematics Matters » Mathematics Matters Case Studies Summary: How Mathematics Is Changing the World

Mathematics Matters Case Studies Summary: How Mathematics Is Changing the World

Every aspect of our modern lives is affected by mathematics. Without mathematics, smartphones wouldn’t work, aeroplanes wouldn’t fly and many common activities such as applying for a credit card would look completely different. When a new technology emerges, few people think about the mathematics that made it possible. The reality is that most innovation simply couldn’t happen without mathematics research.

The Mathematics Matters Case studies were developed by the IMA over a ten-year period to shine a light on the benefits of modern mathematics research, as it was felt that few people outside the scientific community understood its widespread influence.

Mathematics research doesn’t just impact new technologies, it affects society as a whole, with major mathematical innovations happening in healthcare, the environment and even the arts, with the production of most films and video games only made possible due to mathematics. During the Covid-19 crisis, politicians based their decisions on evidence from mathematical modellers, and mathematical terms such as the R number became common place. Even the rise of video calling platforms such as Zoom wouldn’t have been possible without the mathematics underpinning the software.

Mathematics is everywhere – this is why over 60 different Mathematics Matters Case Studies have been produced in conjunction with mathematicians who are experts in their field. Each individual case study is a fascinating insight into one particular application of mathematics, but it is when you look at the whole collection that you start to see the bigger picture and the wide-reaching impact of mathematics.

The economic benefit of mathematics research is also startling – for every £1 invested, there is a £588 return for the economy (compared with Engineering £88, Physics £31, and Chemistry £246 [1] ). It has also been found that an astounding 10% of jobs are linked to mathematical research in the UK [2] . Mathematics not only affects how we live on a daily basis; it is also an economic powerhouse.

Below are some highlights from the series, and a link to the full set of Mathematics Matters Case Studies can be found at the end. Mathematical research is never finished and in the future the IMA will continue to expand the Mathematics Matters Case Studies with cutting edge applications of mathematics.

Health and Medicine

Mathematics is driving big advances in many areas of medicine, but what is surprising is the sheer diversity in its applications. From modelling cancer to developing clearer scan images; even to growing new organs from scratch; mathematics is now fundamental to a lot of healthcare research.

Fighting Cancer With Maths

Mathematicians at the University of St Andrews have developed important new models of how cancer spreads, thereby enabling clinicians to have a better understanding of how to provide more effective treatment for patients.

Tissue Engineering

Scientists are trying to grow replacement organs in the laboratory and mathematics is playing a key role.

Environment

Environmental concerns are high up the agenda, with people around the globe being affected on a daily basis by problems such as flooding and air pollution. Mathematicians are working to address many of these issues, often by using advanced mathematical models.

Natural Flood Management: How Mathematics Can Help Manage the Risks

Academic mathematicians, engineers and environmental scientists have worked with researchers from industry to examine the impact of low-cost nature-based flood defences.

Cleaning up the Air We Breathe: Using Statistics to Understand the Impact of Air Pollution

Air pollution is one of the most important environmental threats to human health. Statisticians at the Universities of Glasgow and Strathclyde have been working to examine the potential impact of the new Glasgow Low Emission Zone.

Architecture and the Built Environment

Mathematics is helping to push the boundaries of modern architecture, not only by creating visually stunning designs, but also addressing other factors such as the effect on the environment and the comfort and safety of the people who live and work in these urban spaces.

Designing the Future: How Mathematics Is Redefining Architecture

Mathematics is revolutionising modern building design. Parametric Models have now been used in the design of many famous buildings such as Dublin’s Aviva Stadium and the roof of the British Museum’s Great Court.

Following the Crowd

London’s annual New Year celebrations are just one example of where the mathematics of crowd dynamics is used. Keeping people safe at large events wouldn’t be possible without the mathematics of crowd control.

Space and Technology

Space technology has always been more easily associated with mathematics, with popular images of rocket scientists working at NASA. The Mathematics Matters Case Studies highlight thriving examples of UK space research which are happening right on our doorstep.

Satellite Communications

Without mathematics, satellites would quickly move out of formation rendering our communications systems useless.

Maths in Space: Mission to Jupiter

Researchers have been using complex mathematical techniques in order to design protection for instruments on board a Jupiter bound spacecraft.

Art and Entertainment

The Arts are often depicted as being far removed from mathematics. The modern reality is that mathematics is helping artists to achieve results which could have only been dreamed about in the past. From film making to art restoration, mathematics is helping the creative industries to produce ever more realistic images.

Maths in the Movies

Maths is used to create many of the special effects that modern films rely on so much. As an example, the Lord of the Rings trilogy used 263 special effects artists, all of whom used a vast amount of maths to do their work.

Filling in the Gaps: The Hidden Role of Mathematics in Art Restoration

Digital restoration offers the only hope of viewing some manuscripts like they might have looked originally. This ‘in-painting’ technique also has a number of other useful applications beyond the world of art restoration, for example in the analysis of fingerprints.

Link to the full series of Mathematics Matters Case Studies

Acknowledgements.

The IMA would like to thank all of the experts and writers who have contributed to the production of the Mathematics Matters Case Studies. In particular they would like to thank Professor Chris Budd OBE, Dr Alan Stevens, Jacob Aron, Colin Stuart and Hazel Lewis.

1. https://epsrc.ukri.org/newsevents/pubs/era-of-maths/

2. https://epsrc.ukri.org/newsevents/pubs/deloitte-measuring-the-economic-benefits-of-mathematical-science-research-in-the-uk/

Related Posts

© 2024 IMA. All Rights Reserved. Site by Measured Designs .