powers of 10 reasoning and problem solving

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Interpret fractions as decimals

Powers of 10

Here you will learn about powers of 10, including what they are and how to write and solve equations using powers of 10.

Students will first learn about powers of 10 as part of numbers and operations in base ten in 5th grade.

What are powers of 10?

Powers of \bf{10} are 10 multiplied by itself over and over again and written with exponents.

For example,

Since our number system is Base 10 (meaning each place value position is grouped by tens), when numbers are multiplied or divided by powers of 10, place value patterns are created.

\begin{aligned} & 67 \times 10=670 \\\\ & 67 \times 10^2=6,700 \\\\ & 67 \times 10^3=67,000 \end{aligned}

The digits from the original number (67) are always in the product, but they increase in place value.

Notice that each time an additional 10 is multiplied, the number of place value positions the digits move increases by one.

This is also true when dividing with powers of 10.

\begin{aligned} & 67 \div 10=6.7 \\\\ & 67 \div 10^2=0.67 \\\\ & 67 \div 10^3=0.067 \end{aligned}

The digits for the original number (67) are always in the quotient, but they decrease in place value.

Notice that each time an additional 10 is divided, the number of places the digits move increases by one.

[FREE] Exponents Check for Understanding Quiz (Grade 4 to 6)

Use this quiz to check your grade 4 to 6 students’ understanding of exponents. 15+ questions with answers covering a range of 5th and 6th grade exponents topics to identify areas of strength and support!

Common Core State Standards

How does this relate to 5th and 6th grade math?

• Grade 5 – Numbers and Operations in Base Ten (5.NBT.2) Explain patterns in the number of zeros of the product when multiplying a number by powers of 10, and explain patterns in the placement of the decimal point when a decimal is multiplied or divided by a power of 10. Use whole-number powers of 10 to denote powers of 10.

How to use powers of 10

In order to represent a number as a power of 10 :

Show the number as an expression with multipliers of \bf{10} .

Count the number of \bf{10} s in the expression to create the power of \bf{10} .

Write the equation.

In order to solve an expression with a power of 10 :

Use place value reasoning to identify how the power of \bf{10} will change the number.

Shift the digits left if multiplying and shift the digits right if dividing.

Powers of 10 examples

Example 1: number as a power of 10.

Write 45,000 as a power of 10.

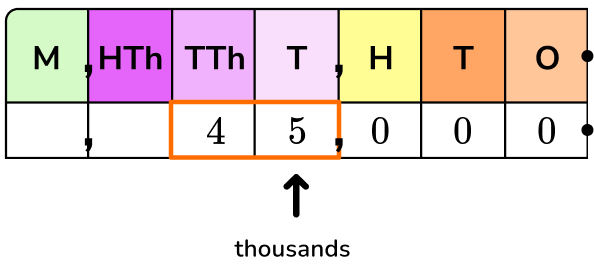
45,000 is the same as 45 thousands or 45 \times 1,000.

1,000 as a product of tens is 10 \times 10 \times 10, so…

45,000=45 \times 10 \times 10 \times 10

2 Count the number of \bf{10} s in the expression to create the power of \bf{10} .

There are 3 tens being multiplied. Use 10 as the base and 3 as the exponent.

3 Write the equation.

45,000=45 \times 10^3

*Note: You can show 45,000 with other powers of 10. See how in the next example.

Example 2: number as multiple powers of 10

Write 1,030,000 as two different powers of 10.

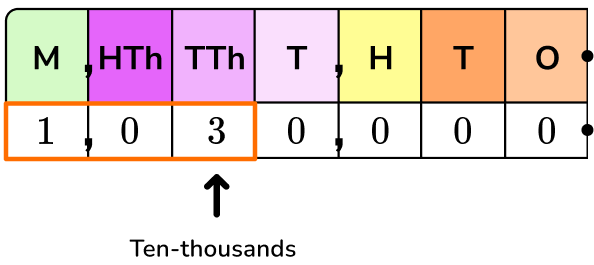
1,030,000 is the same as 103 ten-thousands or 103 \times 10,000.

10,000 as a product of tens is 10 \times 10 \times 10 \times 10, so…

1,030,000=103 \times 10 \times 10 \times 10 \times 10

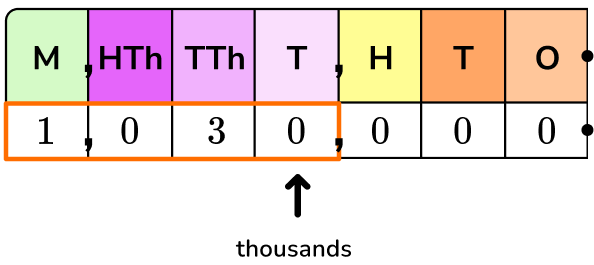
1,030,000 is also the same as 1,030 thousands or 1,030 \times 1,000.

1,030,000=1,030 \times 10 \times 10 \times 10

There are 4 tens being multiplied. Use 10 as the base and 4 as the exponent.

1,030,000=103 \times 10^4

1,030,000=1,030 \times 10^3

*Note: The example shows two possible powers of 10 equations, but any place value can be used to show powers of 10.

Example 3: expression with a power of 10 – product

Solve 5.3 \times 10^6 using place value reasoning.

10^6=10 \times 10 \times 10 \times 10 \times 10 \times 10

Since each place value is 10 times larger than the position to the right, 5.3 will be 6 place value positions larger after it is multiplied by 10^6.

Multiplying by 10, makes a number 10 times larger, which shifts the digits to the left.

For \times 10^6, shift the digits 6 positions to the left.

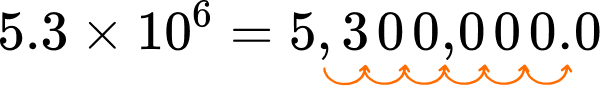
Example 4: expression with a power of 10 – quotient

Solve 80,800,000 \div 10^7 using place value reasoning.

10^7=10 \times 10 \times 10 \times 10 \times 10 \times 10 \times 10

Since each place value is 10 times smaller than the position to the left, 80,800,000 will be 7 place value positions smaller after it is divided by 10^7.

Dividing by 10, makes a number 10 times smaller, shifts the digits to the right.

For \div 10^7, shift the digits 7 positions to the right.

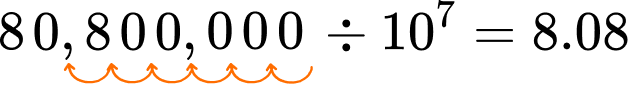
Example 5: expression with a power of 10 – missing operation and power of 10

Complete the equation using an operation with a power of 10 :

The 5 in 5.16 is in the ones position.

The 5 in 51,600 is in the ten-thousands position.

From 5.16 to 51,600 the power of 10 changes the number by 4 place value positions.

This means the power of 10 is 10^4.

The place value of the 5, 1 , and 6 grows larger by 4 positions. Because of this, the digits shift to the left and the operation is multiplication.

5.16 \times 10^4=51,600

Example 6: expression with a power of 10 – missing dividend

Complete the equation:

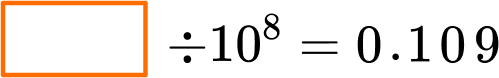
10^8=10 \times 10 \times 10 \times 10 \times 10 \times 10 \times 10 \times 10

Since each place value is 10 times smaller than the position to the left, 0.109 is 8 place value positions smaller than the dividend that was divided by 10^8.

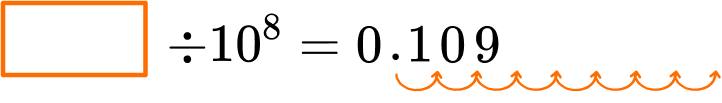
The 1, 0 , and 9 in dividend will be 8 place value positions larger than in the quotient, 0.109.

Even though the equation operation is division, to find the quotient, work backwards and shift the digits to the left.

10,900,000 \div 10^8=0.109

Teaching tips for powers of 10

• Throughout teaching this skill, never forget that the main purpose is for students to explain patterns and deepen their understanding of place value. While the rules “moving the decimal point” or “adding zeros” may come up in discussions, students who memorize these rules and never make place value connections will not truly master the standard – even if they can rotely solve these types of problems.
• Worksheets are useful for this skill, but be sure they include a variety of question types. Worksheets that only include solving for the product or quotient and/or do not ask students to explain the place value connection, will promote only a rote understanding of this skill.

Easy mistakes to make

• Not knowing what to do when there are \bf{0} s within (not just at the end) Students are quick to notice a pattern between the power of 10 and the amount of 0 s at the end of many numbers. However, if students only see numbers that have 0 s at the end, they may create solving strategies that don’t work with all numbers. This could cause mistakes when dealing with numbers like 304,000 or expressions like 5.06 \times 10^4. It is important to expose students to these types of numbers and equations from the beginning, to help avoid this misconception.

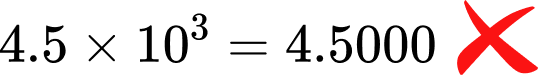
• Forgetting about an exponent of \bf{1} 10 by itself is technically 10^1. It is not typically written this way, but it is important to remember that the exponent of 1 is there.

Related exponents lessons

• Negative exponents

Practice powers of 10 questions

1. Which expression shows 19,000 as a power of 10?

19,000 is the same as 19 thousands or 19 \times 1,000.

19,000=19 \times 10 \times 10 \times 10

19,000=19 \times 10^3

2. Which expression shows 2,030,000 as a power of 10?

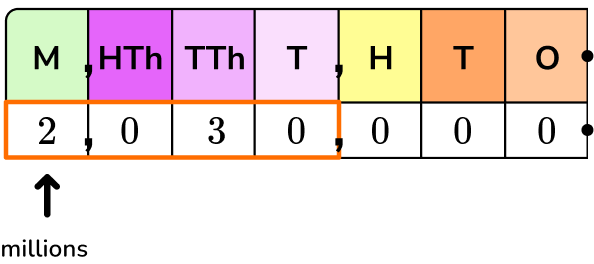
2,300,000 is the same as 2.03 millions or 2.03 \times 1,000,000.

1,000,000 as a product of tens is 10 \times 10 \times 10 \times 10 \times 10 \times 10, so…

2,030,000=2.03 \times 10 \times 10 \times 10 \times 10 \times 10 \times 10

There are 6 tens being multiplied. Use 10 as the base and 6 as the exponent.

2,030,000=2.03 \times 10^6

3. Solve 180 \times 10^5.

10^5=10 \times 10 \times 10 \times 10 \times 10

Since each place value is 10 times larger than the position to the right, 180 will be 5 place value positions larger after it is multiplied by 10^5.

Multiplying by 10, moves all the digits up one position.

For \times 10^5, shift the digits 5 times to the left.

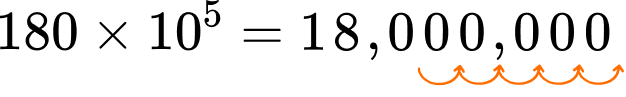
Notice in this case, since 180 is a whole number, that \times 10^5 also “adds” 5 zeros.

This happens for the same reason the decimal point “moves.”

The place value is growing by 5 positions, so each new position needs a 0 as a place holder.

4. Solve 4,100 \div 10^4.

10^4=10 \times 10 \times 10 \times 10

Since each place value is 10 times smaller than the position to the left, 4,100 will be 4 place value positions smaller after it is divided by 10^4.

Dividing by 10, shifts all the digits down one position.

For \div 10^4, shift the digits 4 times to the right.

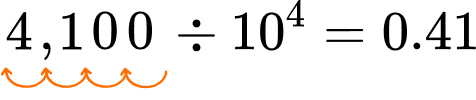
5. Which equation is true?

The 4 in 4.6 is in the ones position.

The 4 in 460,000,000 is in the hundred-millions position.

This is a change of 8 place value positions.

This means the power of 10 is 10^8.

The place value of the 4 and 6 grows larger by 8 positions. Because of this, the digits shift to the left and the operation is multiplication.

6. Which number completes the equation?

10^3=10 \times 10 \times 10

Since each place value is 10 times smaller than the position to the left, 702 is 3 place value positions smaller than the dividend that was divided by 10^3.

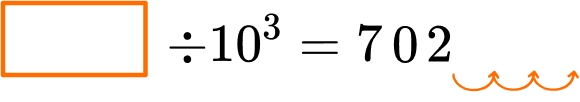
The 7, 0 , and 2 in dividend will be 3 place value positions larger than in the quotient, 702.

702,000 \div 10^3 = 702

Powers of 10 FAQs

For this standard, powers of 10 are useful in identifying and understanding place value patterns. In later grades, this skill is referred to as scientific notation and is used to represent very small numbers and very large numbers in a more efficient way.

The number of times the decimal place moves is the same as the exponent when 10 is the base. The operation, multiplication or division, tells which direction to move the decimal place.

Yes, although this standard only covers positive powers, in later grades, students will work with negative powers of ten.

Per the Common Core, in 5th grade, students work with the tenth, hundredth, and thousandth positions. However, in real world applications, powers of 10 have no limit as to how many decimal points they can represent. It is common that they include numbers up to billionth or even smaller positions. In fact, one of the purposes of powers of 10 is to make it easier to write very, very small numbers.

Yes, scientific calculators in particular include an exponent function that can be used to input and solve an equation with a power of 10.

The next lessons are

• Algebraic expressions
• Math equations
• Inequalities

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview

• About Mrs. Ryder
• Academic Expectations and Routines
• Additional Learning Opportunity
• Online Resourcse
• SOL Objectives and Resources
• SOL Practice
• Jefferson Lab
• Hour of Code
• VDP Summer Academy
• Equivalence and Order of Values
• Scientific Notation
• Squares and Square Roots
• Basics of Powers
• Absolute Values
• Classification
• Arithmetic Basics
• Modeling Operations with Negatives
• Powers with Negative Bases
• Finding Percents
• Change of Percent
• Combining Like Terms
• Inequalities
• Coordinate Planes
• Pythagorean Theorem
• Pairs of Angles
• Quadrilateral Classification
• Surface Area
• Change in Attributes
• Problems with Similar Figures
• Scale Models and Maps
• Transformations
• Introduction to Probability
• Experimental and Theoretical Probability
• Independent and Dependent Events
• Scatterplots

Powers of Ten

Sol objective(s):, the basics and background information, essential knowledge and skills, the topic: what is it and what will we learn.

Filter year:

Powers of 10 Mixed Activity

This Year 6 Powers of 10 resource contains a mix of fluency, reasoning and problem solving questions which will reinforce the skills of multiplying by 10, 100 and 1000. Children will use number grids, function machines and place value charts to spot and continue patterns as well as practise conversion between measurements. Questions such as spotting the odd one out and explaining mistakes will also challenge children to use their reasoning skills.

Curriculum Objectives

• Read, write, order and compare numbers up to 10 000 000
• Solve number and practical problems that involve 6N2 - 6N5

Number and Place Value

More like this

More Y6 resources

• International
• Education Jobs
• Schools directory
• Resources Education Jobs Schools directory News Search

Powers of ten year 6 mastery

Subject: Mathematics

Age range: 7-11

Resource type: Lesson (complete)

Last updated

24 August 2022

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

This follows the White Rose Scheme for year 6 place value. It is understanding the powers of ten. It includes varied fluency, reasoning and problem solving.

Tes paid licence How can I reuse this?

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

This resource hasn't been reviewed yet

To ensure quality for our reviews, only customers who have purchased this resource can review it

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource: